Meta learning quick overview

To mimic the way human perceive, process and associate the previously seen information to better identify the current experience requires ability to extend the information learnt from previous tasks. Human brain is good at propagating the information learnt from one task to adapt to another. As a result, it quickly grasp and understand the concepts with minimal number of examples.

Current deep learning approaches are capable of learning any task provided labeled data is available in abundance and performs poorly where limited training dataset is available. It is therefore of great significance to develop learning algorithms that leverages information gained from a related task and learns efficiently and rapidly when presented with a limited number of training examples (also known as few shot problem).

To address few shot learning meta learning methods have been proposed, broadly categorized as (very well described in 1):

• Metric based methods (focuses on learning similarity metrics between members of the same class)
• Memory based methods (exploits memory baseed architecture to store key training examples)
• Optimization based methods (search for an optimal region in parameter space favorable to fast adaptation of new task)

This blogpost aims to explain the implementation of optimization based method (Specifically known as MAML proposed in 2) applied in the context of few shot learning. MAML aims to find the optimal point in the parameter space which when presented with multiple tasks (limited training examples for each of the task) can easily be adapted to each of these task with few gradient updates and limited training example. Figure below depicts the point in a hyperparameter space (θ of a deep neural network) where the network can easily be trained to each of the three given tasks corresponding to three different directions (θ1, θ2, θ3).

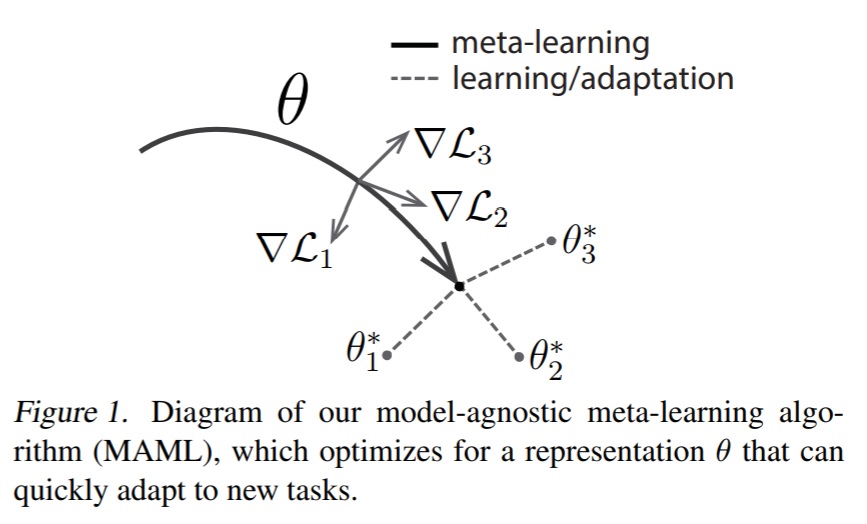
Thus in a meta-learning phase the model aims to identify the parameter Ɵ such that when presented with a new task (or a set of tasks) the parameters can easily be tuned in a few gradient steps.

In training phase the parameter set θ is obtained by evaluating the validation loss over a set of task given as:

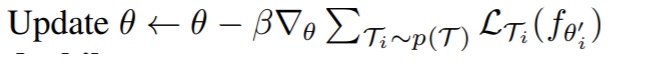
whereas task specific θ’s (such as θ1, θ2, θ3) are obtained as follows (by performing few gradient steps independently over each task using θ as initial starting point):

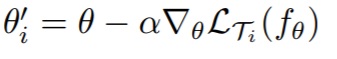
This approach has shown to work well for few shot classification problem such as mini-imagenet. The latest research in this direction is discussed in 3 and improves by a large margin over MAML.

When to use ?

In various industrial application there exist dataset which is not in abundance to fullfill the deep neural network desire to train effectively. Meta learning in such domains become the natural choice to train models which could learn from limited dataset available for different tasks quickly and efficiently. Say a credit card company launhces a new credit card across selective few markets and the datapoints depicting defaulter behavior is emerging (and thus very few), in such scenarios building predictive model using limited datapoints would not work in a traditional way. With meta learning approach each market could be treated as a task and thus the model parameter for each task can be fine-tuned to model defaulter behavior efficiently.

Research along this direction forces me to think if existing classification models (for large labeled training dataset) build this way would be more efficient or not ?