GANs quick recap
GANs as a generative modeling approach has demonstrated the ability to learn an underlying distribution of the partially observed data. This learnt distribution is then applied to generate sample of similar kind thereby benefitting in increasing the data size and its quality. GANs have found useful in several applications (not limited to):
- Image enhancement such as super resolution
- Style transfer
- Healthcare such as drug discovery
In this blog lets walkthrough how GANs are used to impute missing observations also known as incomplete data. More specifically I am referring to recent article published at ICLR 2019 1
It utilizes following three pairs of Generators and discriminators:
- learning the distirbution of missing values
- learning the distribution of incomplete target data
- Imputer which imputes the missing observation in observed dataset
How it works ?
Given a set of incomplete observations, a mask is defined as below (zero if observation is missing and 1 otherwise). m Є {0,1}
An incomplete dataset can now be represented as:
D = {(xi, mi)} where i Є 1,...,N
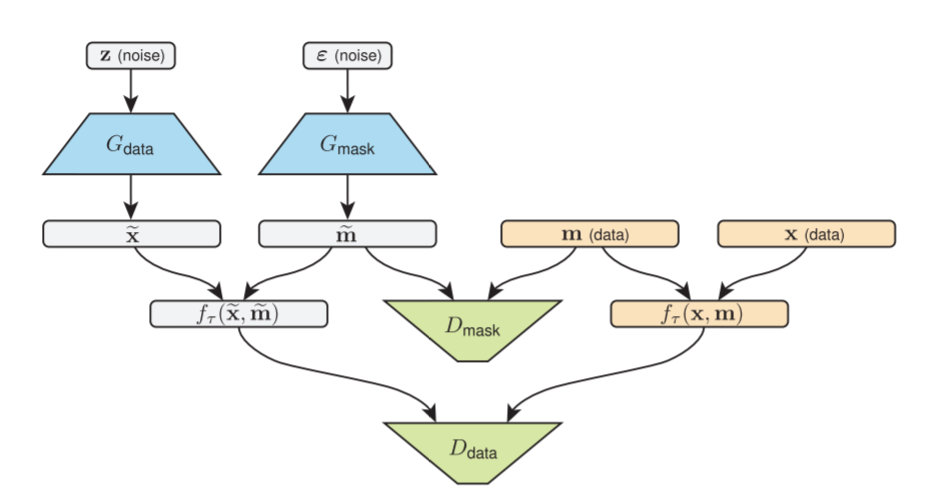
Lets talk about how GANs learns the distribution of location of missing values in an incomplete dataset. Given an input sampled from a distribution known apriori, generater Gmask generates samples which are then fed to discriminator along with masked data derived from observed data. Masked data contains 1s in place where data is observed and 0 otherwise. In this process generator learns to map the apriori distribution to a masked data distribution and adjust its weights so as to be able to locate position of missing values in an observed data.
Loss for this GAN (am referring here as GANmask) is defined as below:
![]()
Another set of GAN (referred as Gdata & Ddata) learns to generate complete observation using incomplete dataset. As usual with GAN training, generator here learns to generate samples (closer to the incomplete data) through an adversarial process where discriminator attempts hard to discriminate between generated samples and observed data. The input to the discriminator is slightly modified using masked operator (defined below):
![]()
Here ̃m represents the compliment of m and is used to fill location of missing values with a constant. The training loss for this GAN now becomes:
![]()
As seen above the combined output of Gmask and Gdata becomes fake sample for discriminator to discriminate against the real data slightly modified using the masking operator (shown above).
Thus the final training objective of GANmask and GANdata now becomes as below:
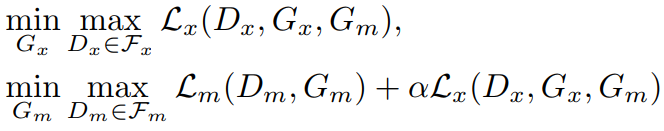
Imputing missing values in observed data
With the above configuration GANs now would be able to learn the distribution of missing values and generate complete data. Something that interests a lot is to be able to impute missing values in place on a given incomplete data. For this another GAN known as imputer is trained (depicted below):
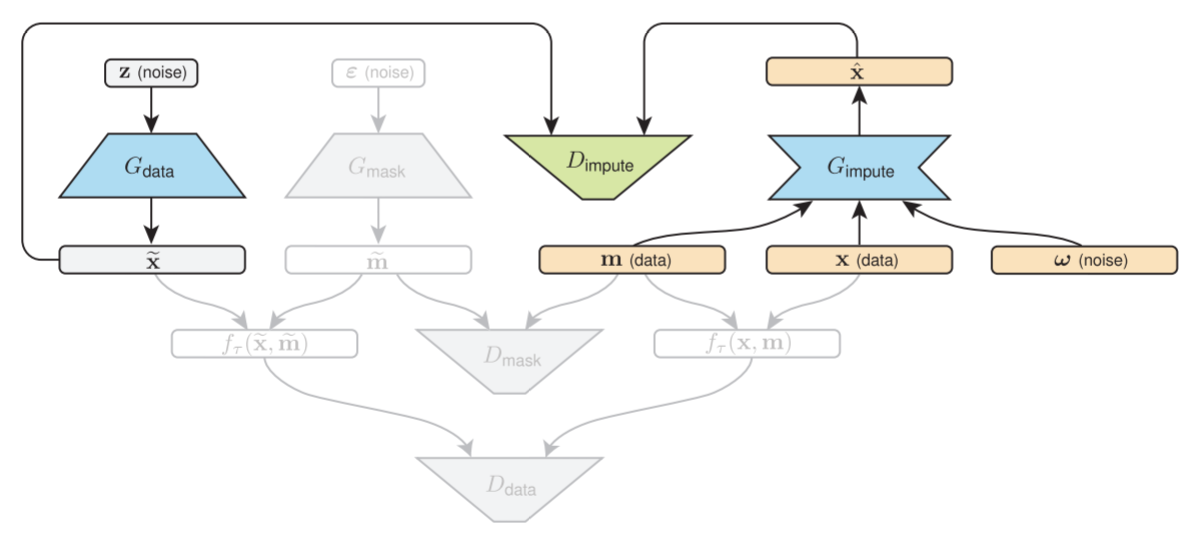
Generator (Gimpute here) takes real data (incomplete) along with some noise and learns to generate samples with following characteristics:
- observed values are kept intact
- missing locations are imputed
Whereas the discriminator learns to discriminate between generated samples (that comes from Gdata) and Gimpute (illustrated in figure above). For imputer GAN loss is defined as below:
![]()
The joint learning for generating process and imputer is defined as according to the following objectives:
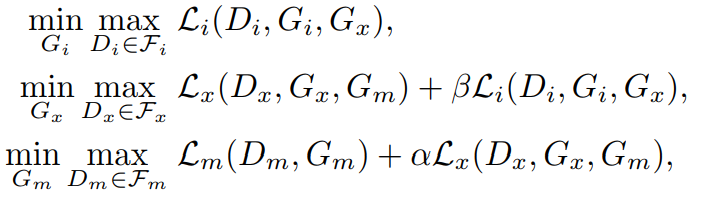
The whole architectural approach to use GANs for missing value imputation looks quite convincing. Lets have a look at how this approach compares against some of the benchmarks. Below depcicts the performance comparison of how well MisGAN (as referred here in this paper 1) imputes missing value and is able to generate clear digits where other methods looks to struggle.

For more indepth details I would recommend to read this interesting paper which got accepted at ICLR-2019 1
As always Happy reading !!